Failure is an option:
Task and Motion Planning with Failing Executions
Abstract: — Future robotic deployments will require robots to be capable of solving a variety of tasks in a specific domain, and be able to repeatedly service such requests. Task and motion planning addresses complex robotic problems that combine discrete reasoning over states and actions and geometric interactions during action executions. Moving beyond deterministic settings, stochastic actions can be handled by modeling the problem as a Markov Decision Process. The underlying probabilities however are typically hard to model since failures might be caused by hardware imperfections, sensing noise, or physical interactions. We propose a framework to address a task and motion planning setting where actions can fail during execution. For a task goal to be achieved actions need to be computed and executed despite failures. The robot has to infer what actions are robust and for each new problem effectively choose a solution that reduces expected execution failures. The key idea is to continually recover and refine the underlying beliefs associated with actions across multiple different problems in the domain to find solutions that reduce the expected number of discrete, executed actions. Results in physics-based simulation indicate that our method outperforms baseline replanning strategies to deal with failing executions.
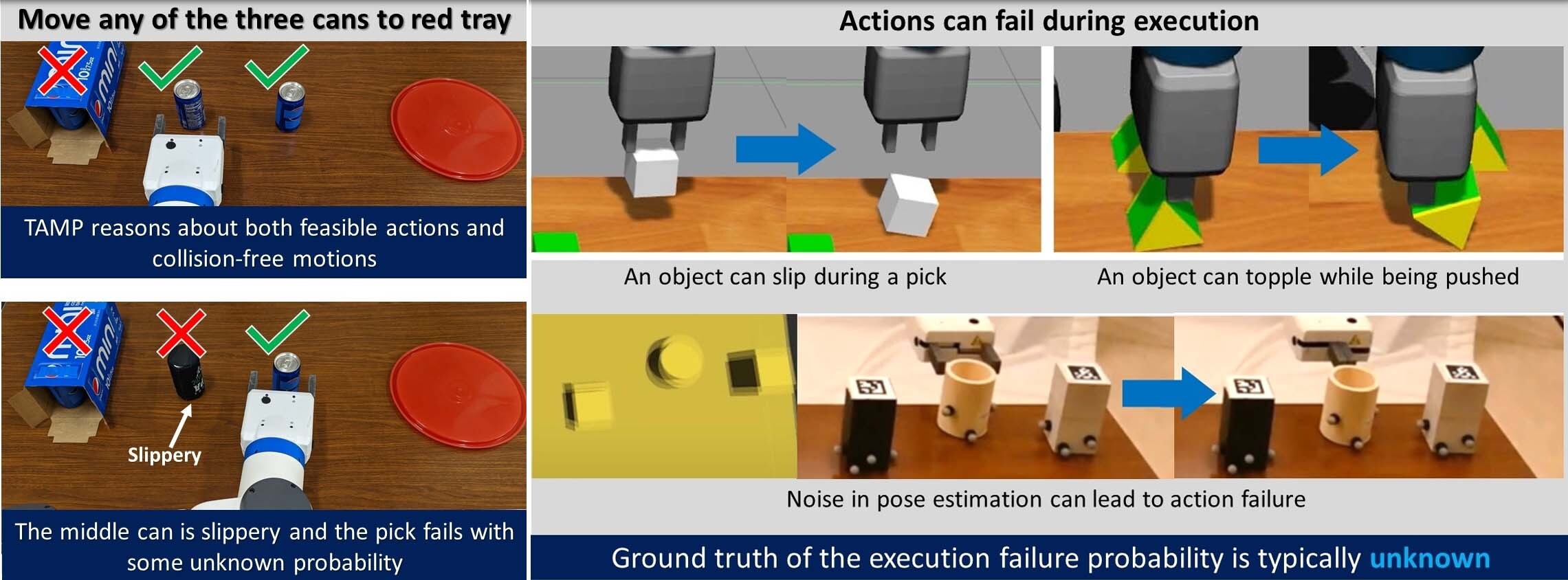
Fig 1: Left: An example task where the goal is to move any one of the three cans to the red tray. Left-Top: A typical TAMP solver discovers the motion constraint that the can inside the box cannot be reached. A feasible plan would be to move one of the right two cans. Left-Bottom: A feasible task and motion plan may fail in execution (e.g., if the middle can is slippery and falls from the gripper). An execution-failure-aware TAMP planner should prefer the rightmost can. Right: Actions can fail during execution due to unknown system errors, nmodeled physical interactions, malfunctioning hardware, noise in pose estimation, etc. Ground truth of the execution failure probability is typically unknown.
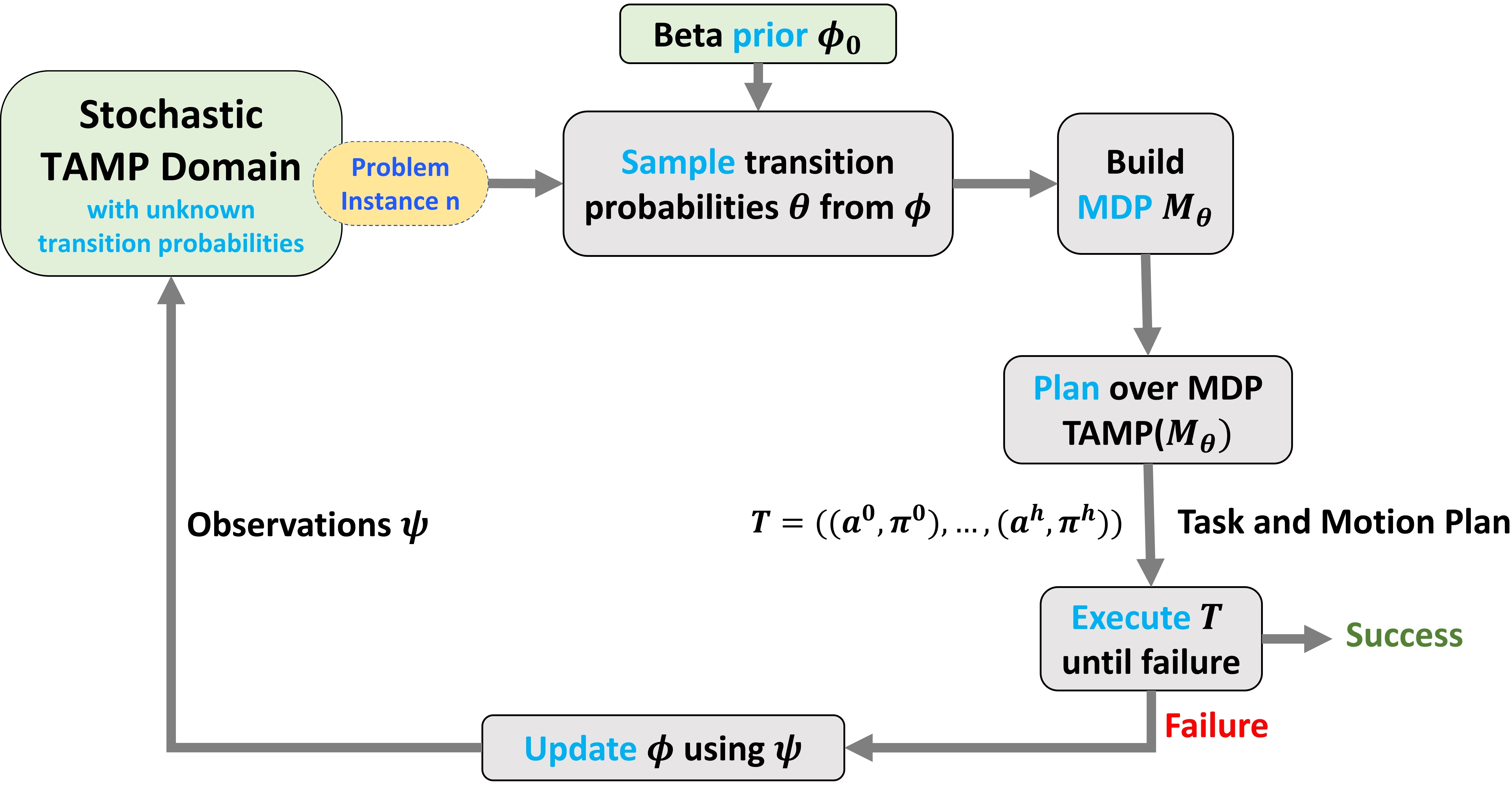
Fig 3: The proposed framework. The stochastic domain is modeled as a Markov Decision Process (MDP) with unknown transition probabilities. We maintain a belief distribution for each transition probability. Posterior sampling is leveraged to balance exploration and exploitation. At each iteration, we plan over the sampled MDP, execute the plan, and collect observations to update the belief, until a problem instance is solved. The belief is maintained across different problem instances in the domain.
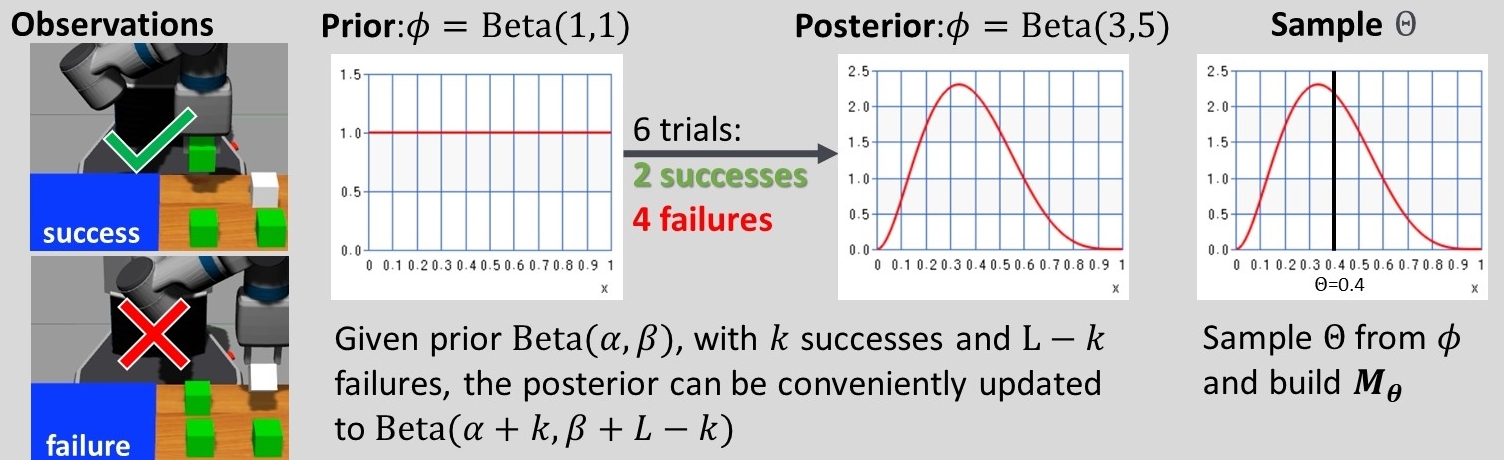
Fig 4: Example of how the belief is updated. Left: Execution success and failure. Middle: An example of how we update the belief distribution of the probability of successfully picking-up a cube. We use Beta distribution for the belief and Binomial for the likelihood. As Beta and Binomial distributions form a conjugate pair, we can update the posterior conveniently. Right: An example of a sampled probability which we can use to construct the MDP.
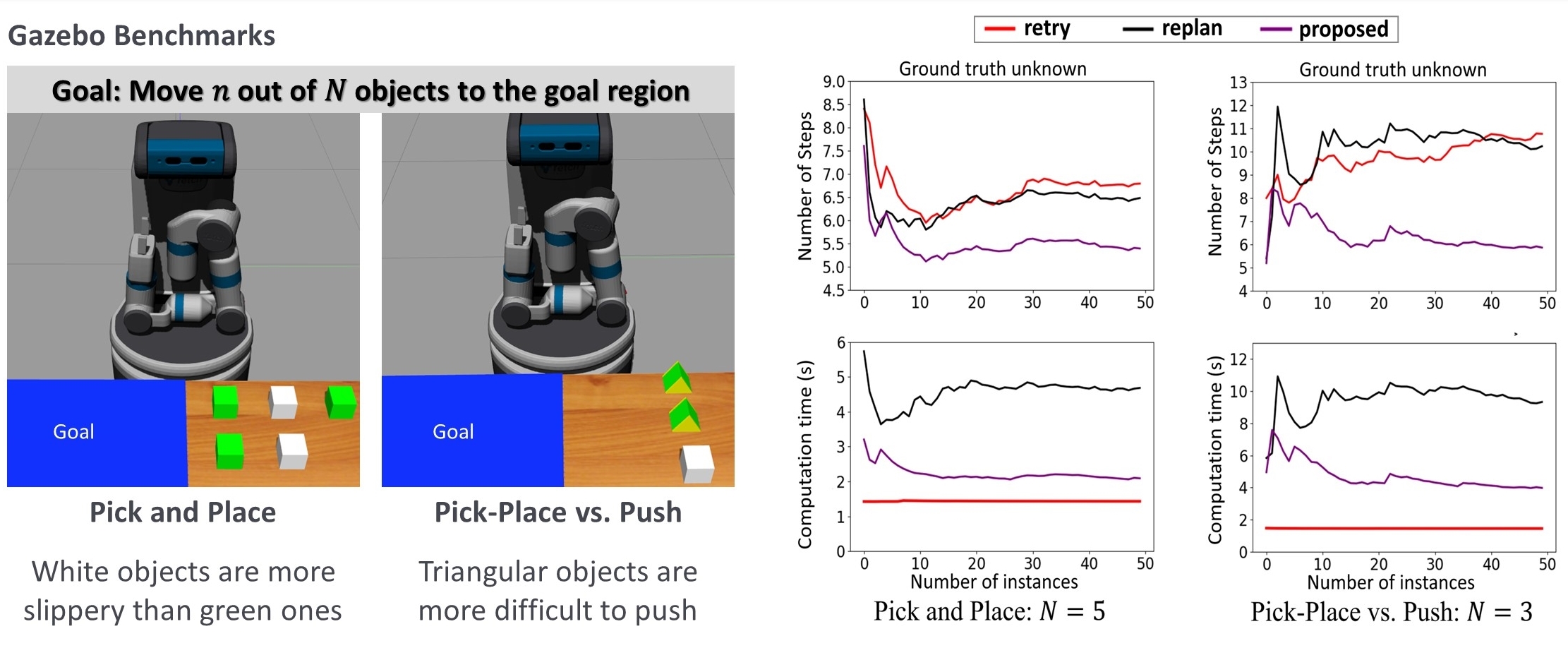
Fig 5: Left: Gazebo benchmark problems. The goal is to move some of the objects to the goal region, allowing a different problem instances in the domain. In the Pick and Place benchmark, white objects are more slippery. In the Pick-Place vs. Push benchmark, the triangular objects are more difficult to push. We tune parameters such as friction coefficients, masses, etc. for the physics simulation in Gazebo. Right: The benchmarking results of the baseline methods. The Retry method retries a failed execution until it succeeds. The Replan method replans upon failure, with the failed action blocked. The Proposed method updates the belief when the execution of an action fails.
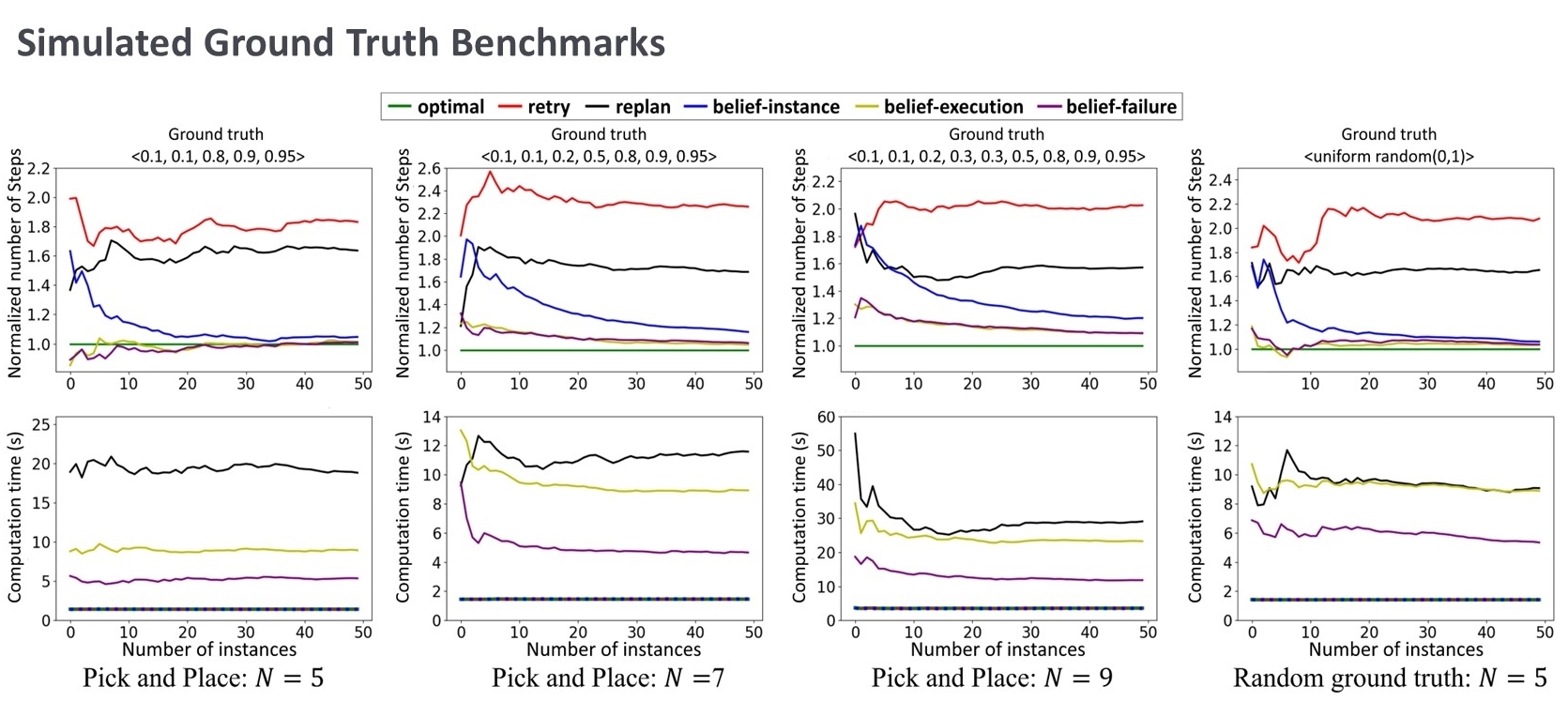
Fig 6: The results of the simulated ground truth benchmark. Here we have an optimal baseline. Two variants of the proposed method are evaluated with belief updates after each action execution or after each problem instance. All the proposed methods converge but show tradeoffs arising from frequency of belief updates.
Rice University Houston TX USA